并查集定义

  1. 并查集是一种树型的数据结构，用于处理一些不相交集合（disjoint sets）的合并及查询问题。
  2. 并查集通常包含两种操作
    1. 查找(Find)：查询两个元素是否在同一个集合中
    2. 合并(Union)：把两个不相交的集合合并为一个集合

并查集思想

请看以下示例：116. 省份数量

有n个城市，其中一些彼此相连，另一些没有相连。如果城市a与城市b直接相连，且城市b与城市c直接相连，那么城市a与城市c间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给出一个n x n的矩阵isConnected，其中isConnected[i][j] = 1表示第i个城市和第j个城市直接相连，而isConnected[i][j] = 0表示二者不直接相连。

给出任意的两个城市i和j，判断是否为同一省份。

并查集的思想就是将每个城市看作一个节点，如果节点之间有联系，那么就选择一个节点为其父节点，例如：

img

若节点0和1有关联，那么随机选择0作为1的父节点：

img

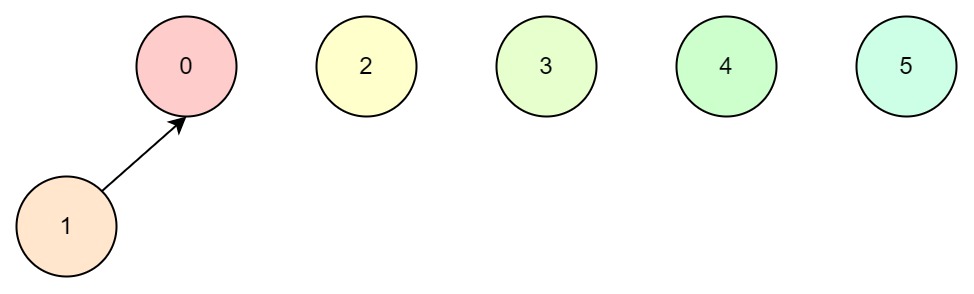
若1和2有关联，那么就找到1的根节点0，即0与2有关联，随机选择0作为父节点：

img

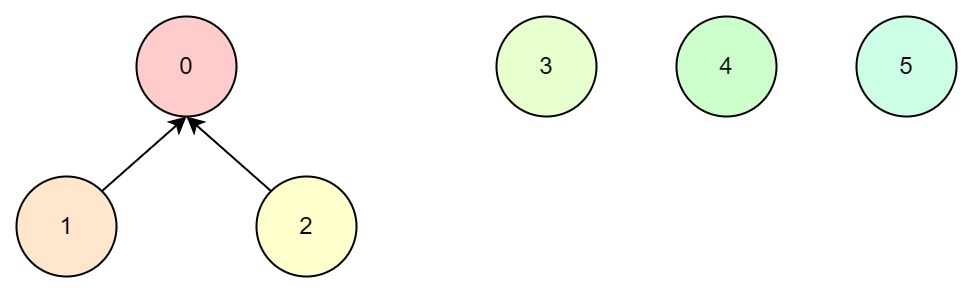
同理，3与4有关联，我们选择4为父节点：

img

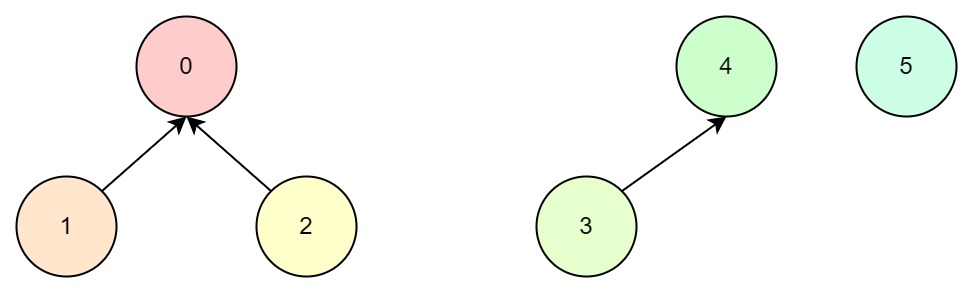
3与5有关联，那么就找到3的根节点4，即4与5有关联，我们选择5为父节点：

img

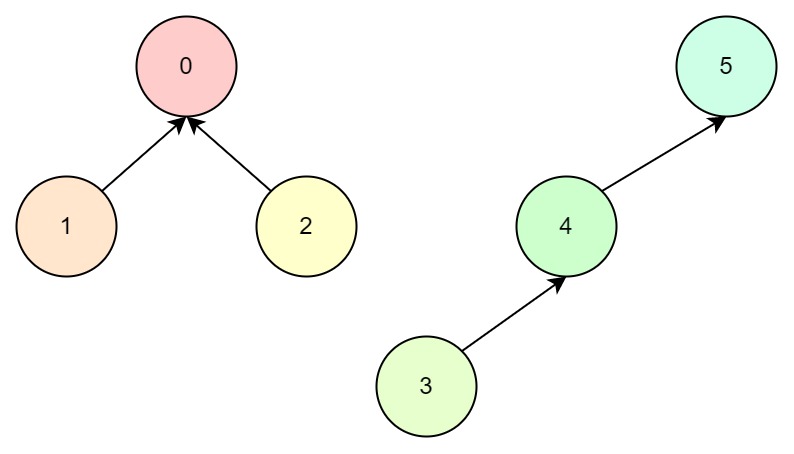
最后2与4有关联，那么我们找到2的根节点0，4的根节点5，随机选择5为根节点：

img

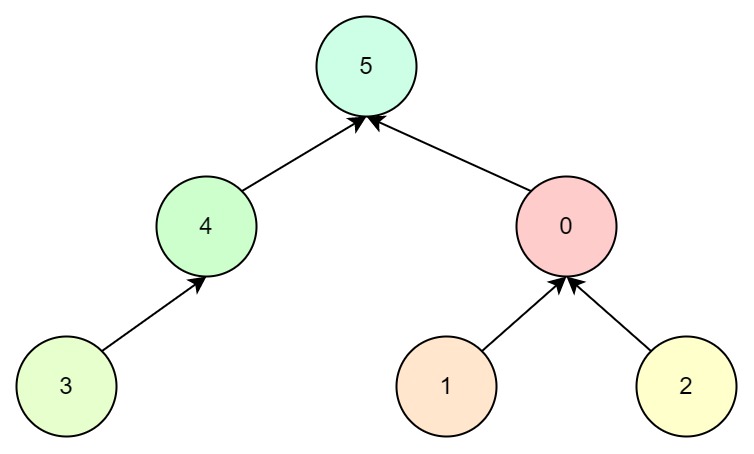
最后所有节点都变成一棵树了，那么如何判断随机给出的两个节点是否为同一集合呢？其实只需要找到其根节点，判断根节点是否一致即可。

并查集的思想就是将每一个不同的集合抽象成一棵棵不同树，对于任意的两个节点，查找其根节点，判断其根节点是否一致即可判断这两个节点是否在同一集合中。

这种算法相对于深度查找与广度查找这种遍历来讲，它只需要朝一个方向去找，在优化树的高度情况下，查找效率更高；而深度广度查找需要查询所有关联的节点，效率相对较低。

并查集代码

初始化

在实现并查集的时候使用数组即可：

1
parent[i] = j

其中parent数组下标i代表当前节点，j代表此节点的父节点下标。

例如：

1
parent[0] = 1

代表下标为0的节点的父节点为下标为1的节点。

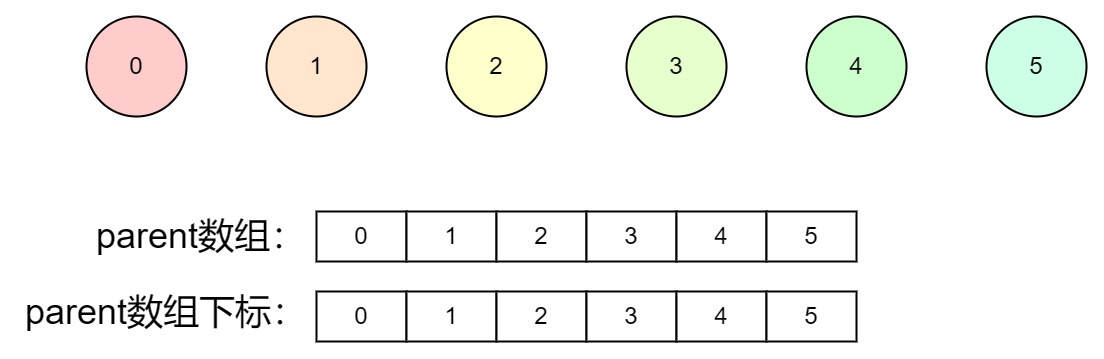
在初始化的时候我们设置每个节点的父节点为当前节点。

1
2
3
4
5
6
7
8
9
10
11
12
int[] parent;

/**
 * 初始化当前节点父节点为当前节点
 * @param n
 */
public void init(int n) {
    parent = new int[n];
    for (int i = 0; i < n; i++) {
        parent[i] = i;
    }
}

此时节点示意图如下：

img

查找

查找方法的目的是查找某个节点的根节点，我们可以使用递归查询。如果当前的根节点的父节点为自身则返回，否则递归查询父节点的根节点。

1
2
3
4
5
6
7
8
9
10
11
12
/**
 * 递归查询根节点
 *
 * @param index
 * @return
 */
public int find(int index) {
    if (parent[index] != index) {
        return index;
    }
    return find(parent[index]);
}

要判断两个元素是否属于同一个集合，只需要看它们的根结点是否相同即可。

img

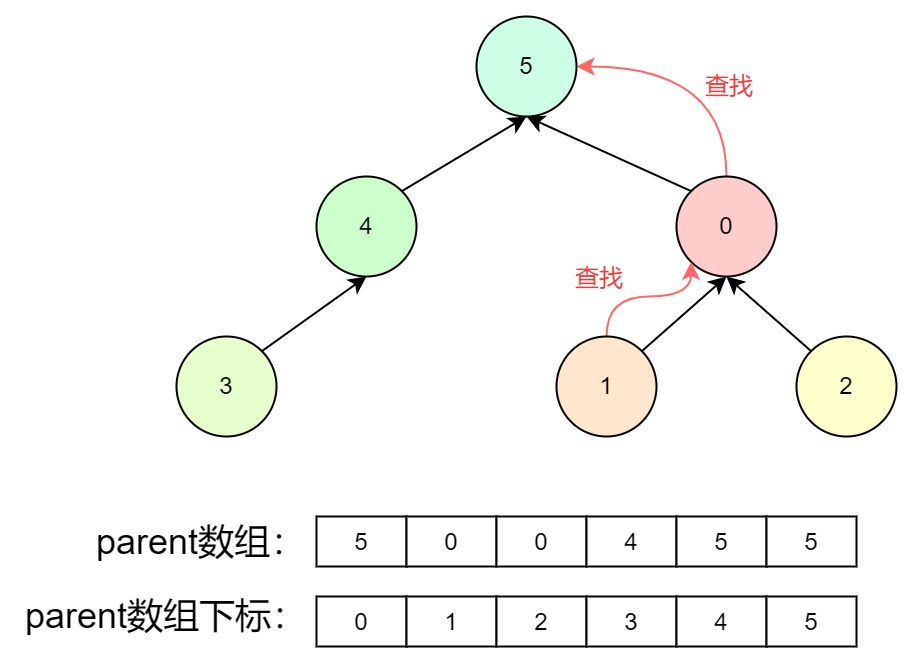
例如我们要查找1节点的根节点：

  1. 判断1节点的父节点是否为本身，1节点的父节点为0，不是本身
  2. 判断0节点的父节点是否为本身，0节点的父节点为5，不是本身
  3. 判断5节点的父节点是否为本身，是，返回

合并

要合并i节点与j节点，并不是直接合并，而是找到其根节点再进行合并。

1
2
3
4
5
6
7
8
/**
 * 合并节点，将i节点的根节点的父节点设置为j节点的根节点
 * @param i
 * @param j
 */
public void merge(int i, int j) {
    parent[find(i)] = find(j);
}

例如当前节点状态如下：

img

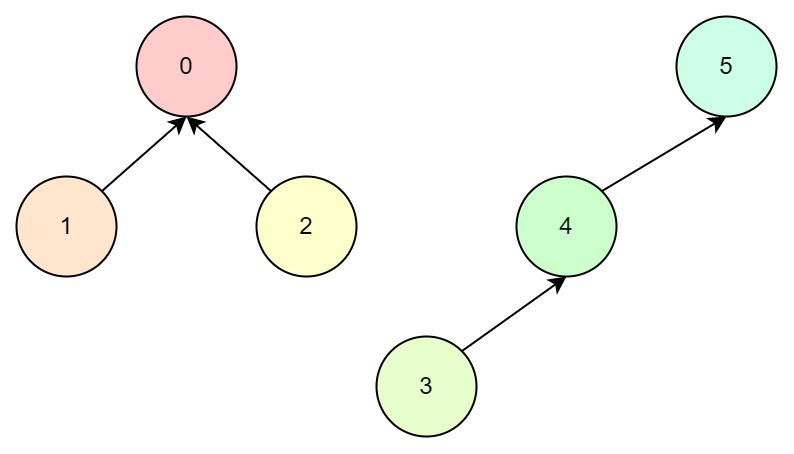
要合并2和4节点，那么我们找到2的根节点0，4的根节点5，再进行合并：

img

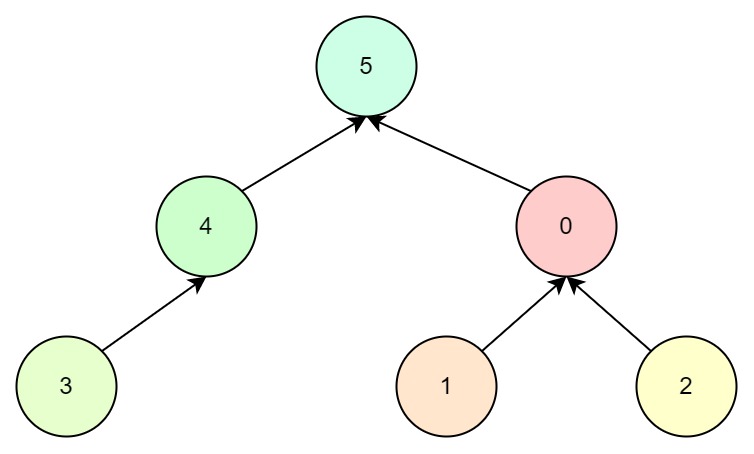
那么我们直接合并2和4节点会怎样呢？

img

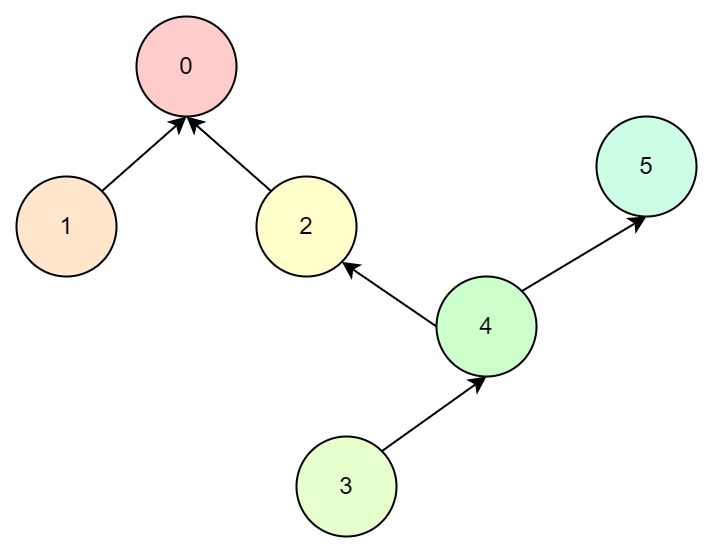
我们发现上图中4节点有两个父节点，那么我们没法保证任意节点都有唯一的根节点，也就没法利用比较根节点这样的性质去判断两个节点是否为同一集合了。

代码

目前为止，并查集的完整代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public class DisJointSetUnion {

    int[] parent;

    /**
     * 初始化当前节点父节点为当前节点
     *
     * @param n
     */
    public void init(int n) {
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
    }

    /**
     * 合并节点，将i节点的根节点的父节点设置为j节点的根节点
     * @param i
     * @param j
     */
    public void merge(int i, int j) {
        parent[find(i)] = find(j);
    }

    /**
     * 递归查询根节点
     *
     * @param index
     * @return
     */
    public int find(int index) {
        if (parent[index] != index) {
            return index;
        }
        return find(parent[index]);
    }
}

并查集优化

路径压缩

路径压缩主要是压缩树的高度，用于提高并查集的效率。

考虑以下场景：

img

所有节点退化成了链表，这样还不如每个每个节点与其根节点直接产生联系：

img

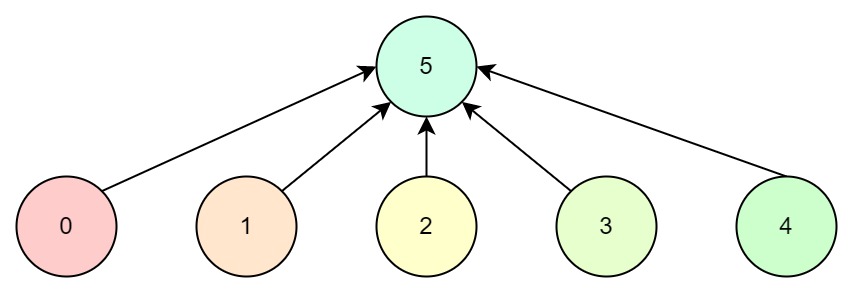
这样查询效率更高。

我们可以考虑在查找的过程中，把沿途节点的父结点都设为根结点，进行路径压缩。

1
2
3
4
5
6
7
8
9
10
11
12
13
/**
 * 递归查询根节点
 *
 * @param index
 * @return
 */
public int find(int index) {
    if (parent[index] != index) {
        // 路径压缩
        parent[index] = find(parent[index]);
    }
    return parent[index] ;
}

这样一来，从查找的当前节点到根节点这一条路径都会被压缩，为后续的查询提高效率。

按秩合并

路径压缩只在查找的时候进行，也只压缩一条路径，所以并查集的最终结构仍然可能是比较复杂的，除非我们定时去压缩所有路径，例如：

1
2
3
4
5
6
7
8
9
10
/**
 * 压缩所有路径
 *
 * @return
 */
public void compress() {
    for (int i = 0; i < parent.length; i++) {
        find(i);
    }
}

假设，我们现在有一颗比较复杂的树，需要和一个单个元素的集合进行合并，需要如何选择根节点？

img

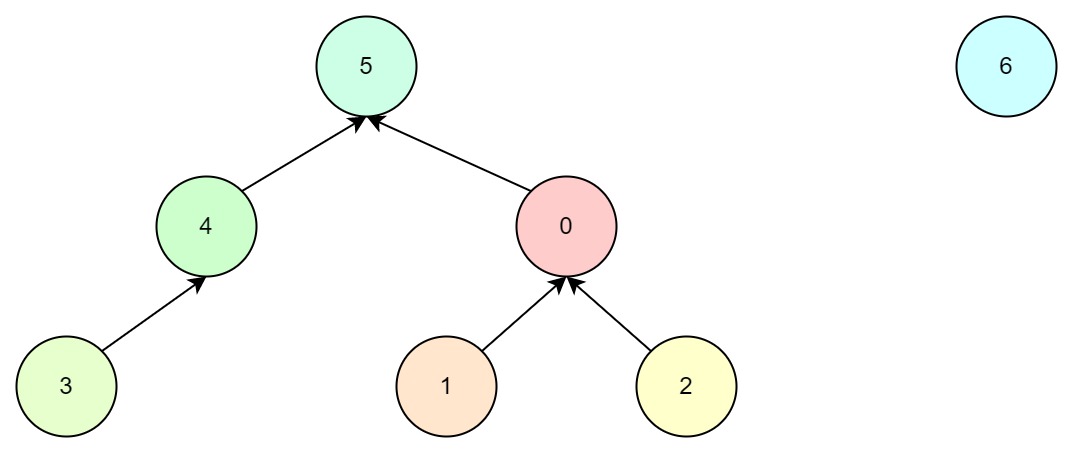
  1. 如果选择6为根节点，最终的树结构如下：

img

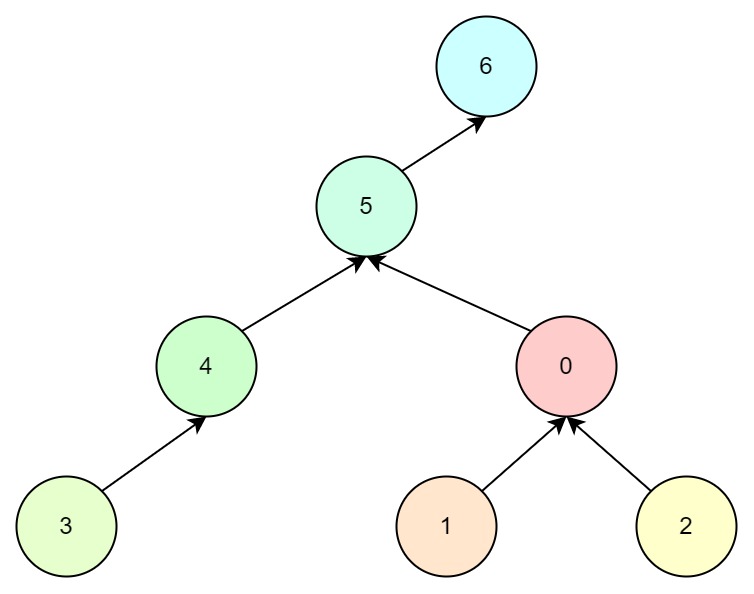
  1. 如果选择5为根节点，最终的树结构如下：

img

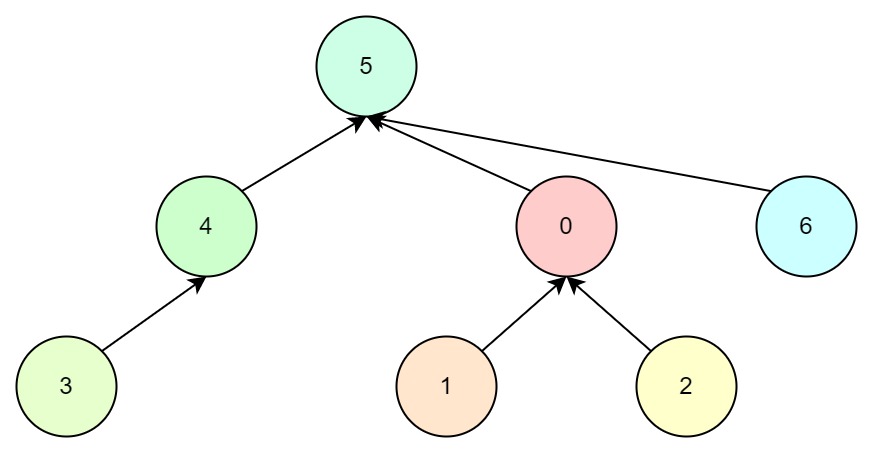
观察以上两种情况，我们发现第一种方式树的深度变高了，这意味着查询效率将会降低，而第二种方式树的高度不变。这启发我们要把深度小的树合并到深度大的树中。

具体做法为：

用rank[]数组来记录每个根结点对应的树的深度（如果不是根结点，则rank中的元素大小表示的是以当前结点作为根结点的子树的深度）；一开始，把所有元素的rank设为1，即自己就为一颗树，且深度为1；合并的时候，比较两个根结点，把rank较小者合并到较大者中去。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
 * 合并节点，将i节点的根节点的父节点设置为j节点的根节点
 *
 * @param i
 * @param j
 */
public void merge(int i, int j) {
    int x = find(i), y = find(j);
    if (x != y) {
        // 按秩合并
        if (rank[x] < rank[y]) {
            parent[x] = y;
        } else {
            parent[y] = x;
        }
        // 如果深度相同，深度+1
        if (rank[x] == rank[y]) {
            rank[x]++;
        }
    }
}

值得注意的是，两个节点深度相同时，才增加某个节点的深度，如果不相同，合并后两个节点的深度都不变。

  1. 深度相同，进行合并，合并后深度+1

img

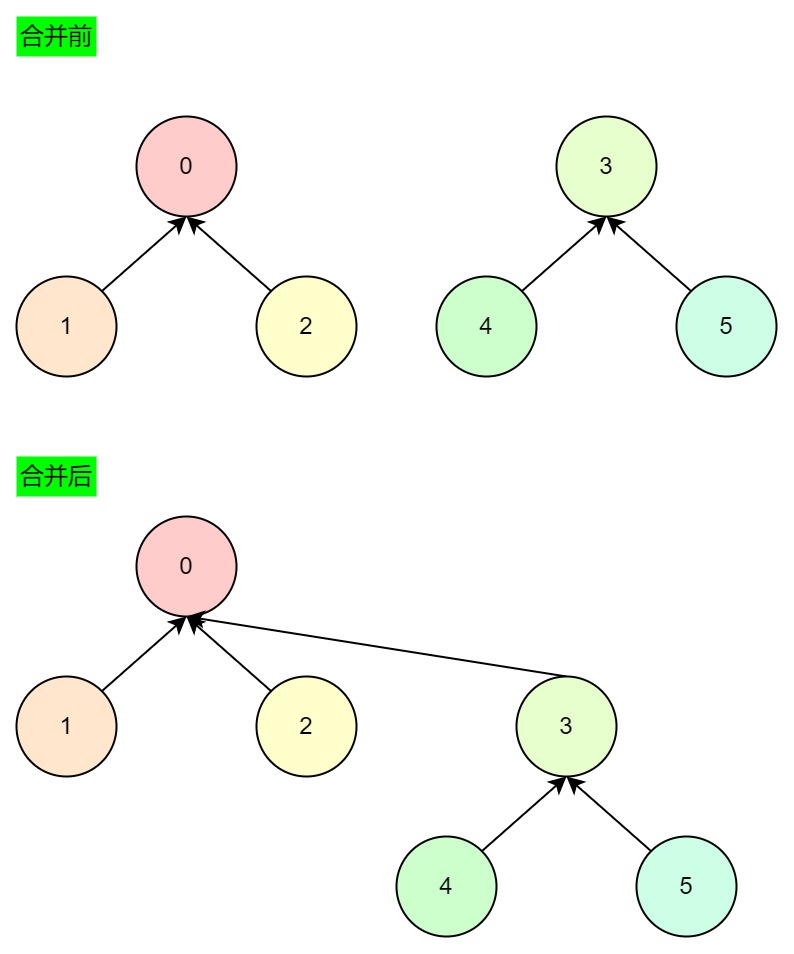
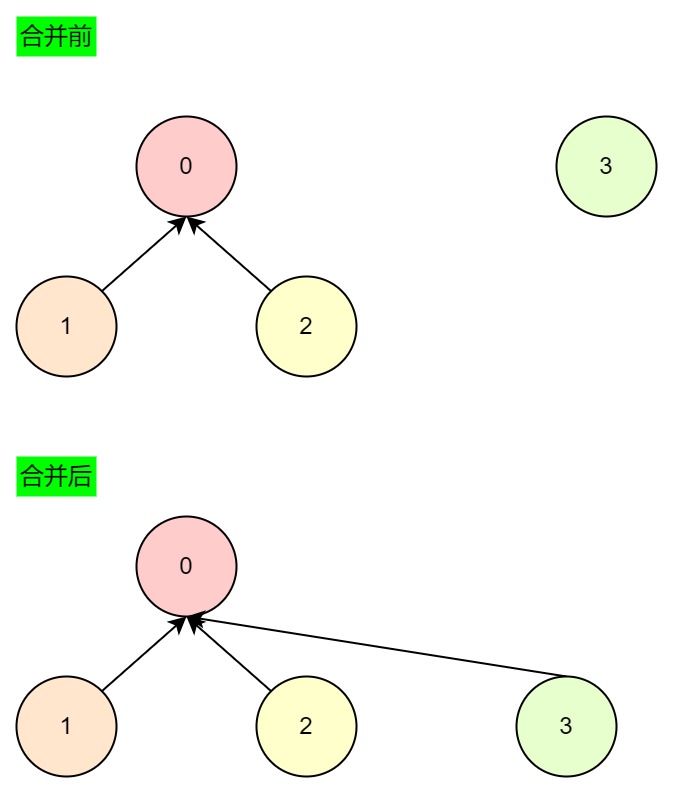
  1. 深度不同，进行合并，深度小的节点合并到深度大的节点上，合并后深度不变

img

代码通用模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
public class DisJointSetUnion {

    int[] rank;
    int[] parent;

    /**
     * 初始化当前节点父节点为当前节点，初始化深度
     *
     * @param n
     */
    public void init(int n) {
        parent = new int[n];
        for (int i = 0; i < n; i++) {
            rank[i] = 1;
            parent[i] = i;
        }
    }

    /**
     * 合并节点，将i节点的根节点的父节点设置为j节点的根节点
     *
     * @param i
     * @param j
     */
    public void merge(int i, int j) {
        int x = find(i), y = find(j);
        if (x != y) {
            // 按秩合并
            if (rank[x] < rank[y]) {
                parent[x] = y;
            } else {
                parent[y] = x;
            }
            // 如果深度相同，深度+1
            if (rank[x] == rank[y]) {
                rank[x]++;
            }
        }

    }

    /**
     * 递归查询根节点
     *
     * @param index
     * @return
     */
    public int find(int index) {
        if (parent[index] != index) {
            // 路径压缩
            parent[index] = find(parent[index]);
        }
        return parent[index];
    }

    /**
     * 压缩所有路径
     *
     * @return
     */
    public void compress() {
        for (int i = 0; i < parent.length; i++) {
            find(i);
        }
    }
}