题目描述

题目链接：124. 二叉树中的最大路径和

路径被定义为一条从树中任意节点出发，沿父节点-子节点连接，达到任意节点的序列。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个节点，且不一定经过根节点。

路径和 是路径中各节点值的总和。

给你一个二叉树的根节点 root ，返回其最大路径和。

示例1：

1
2
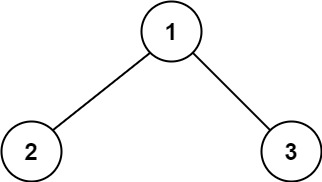
3

输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例2：

1
2
3

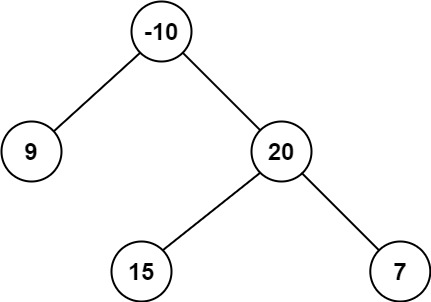
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：

树中节点数目范围是 [1, 3 * 10(4)]
-1000 <= Node.val <= 1000

我的题解

方法一：递归

思路

由题意可知，最大路径的组成可能为：

根节点+左子树+右子树
根节点+左子树
根节点+右子树
根节点
左子树
右子树

因此我们应该考虑根节点是否选择的问题，递归返回值定义为当前树最大的路径（注意不要带根节点），然后在遍历过程中我们取最大值，即为整棵树的最大路径。

而当前树的最大路径为：

根节点
左子树+根节点
右子树+根节点

的最大值，在求整棵树路径的最大值时，我们要再加上根节点判断。

代码

class Solution {

    private int result = Integer.MIN_VALUE;

    public int maxPathSum(TreeNode root) {
        dfs(root);
        return result;
    }

    private int dfs(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int left = dfs(root.left);
        int right = dfs(root.right);
        int max = root.val;
        max = Math.max(max, left + root.val);
        max = Math.max(max, right + root.val);
        result = Math.max(Math.max(result, max), left + right + root.val);
        return max;
    }
}